First editiion. The work “De Maximis et Minimis” by Vincenzo Viviani is of considerable importance in the history of mathematics because it represents one of the first fundamental works on analysis and infinitesimal calculus.
Vincenzo Viviani (1622-1703) was an Italian mathematician, a student of Galileo Galilei and a friend of Evangelista Torricelli. In addition to the development given to geometry, he first measured the arc of a pendulum, one of the first experimental tests of Galileo’s theory, thus contributing to the understanding of the movement of pendulums.
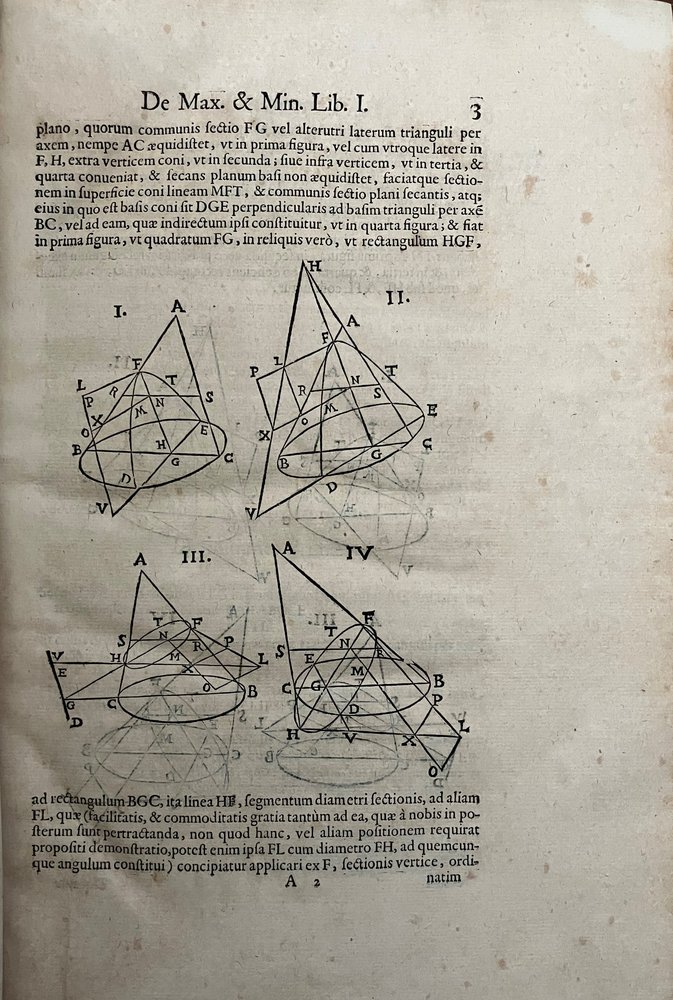
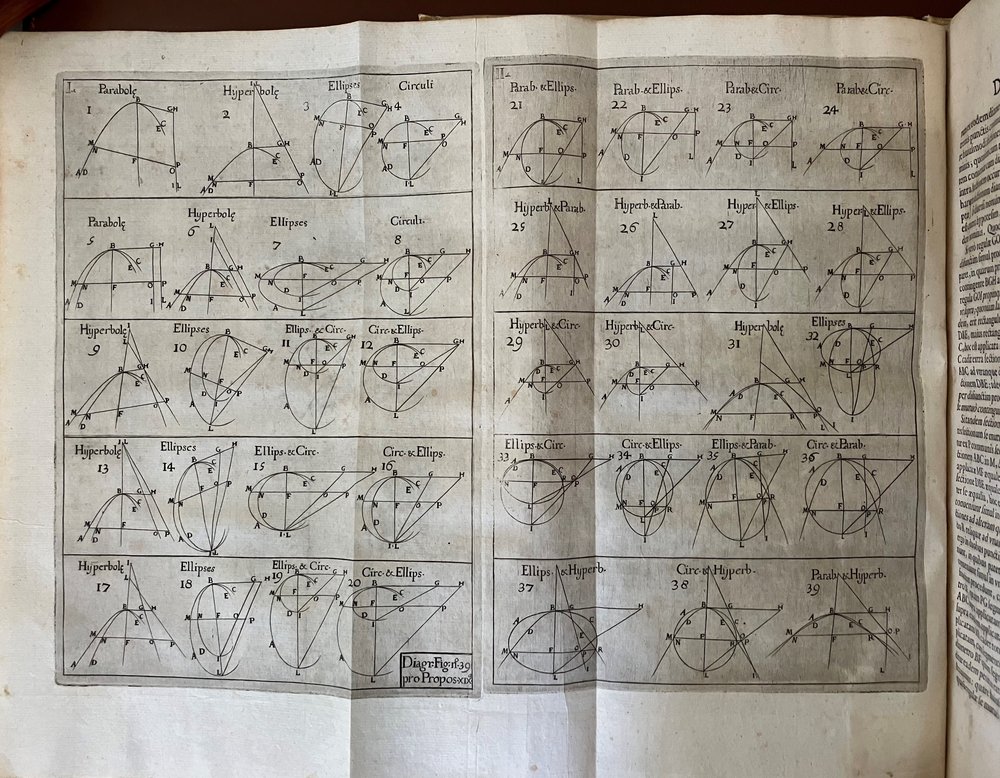
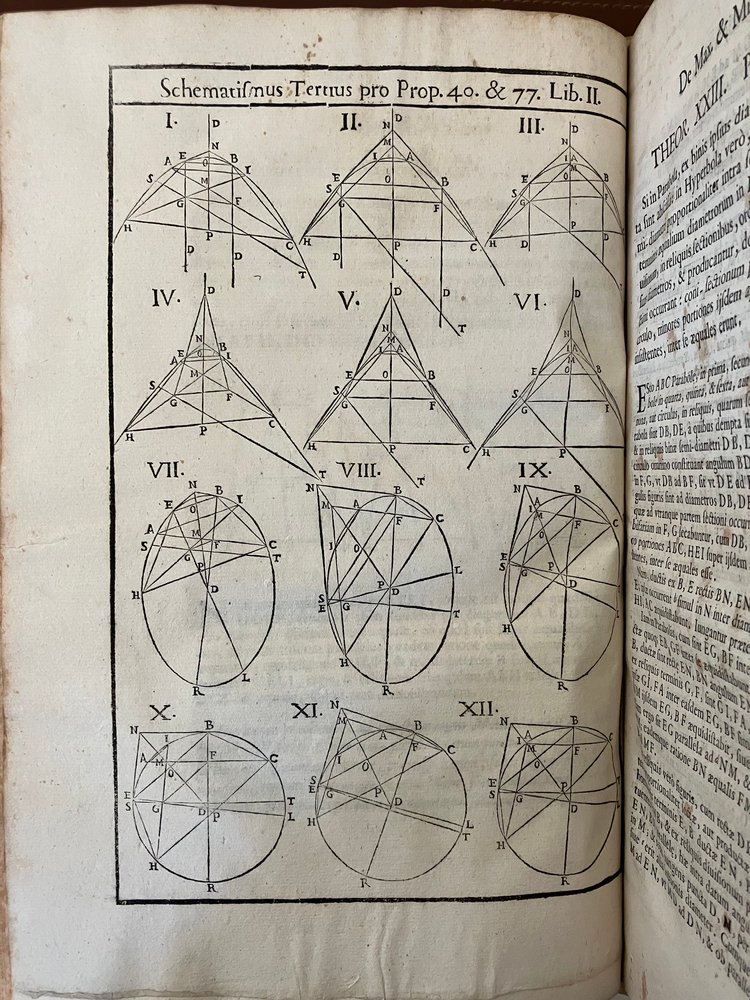
In his work “De Maximis et Minimis”, published for the first time in 1659, Viviani deepens the concepts of maxima and minimums of both algebraic and geometric functions.
«De Maximis et Minimis » is one of the first mathematical treatises to systematically address infinitesimal calculus, a field of mathematics that would become fundamental over the following centuries. Viviani introduces methods to calculate maxima and minima of functions through the analysis of their derivatives, anticipating key concepts of differential and integral calculus.
In his treatise, Viviani does not limit himself to exposing abstract theories, but also proposes concrete solutions to optimization problems, which find application in different disciplines such as engineering, architecture and physics.
“De Maximis et Minimis” greatly influenced the development of 17th century European mathematics. Viviani’s ideas were an important contribution to the development of calculus, a mathematical field that would reach its peak with the work of mathematicians such as Isaac Newton and Gottfried Leibniz in the following century.
Bibliography: Cinti 135. – Riccardi I/2, 625 (“raro e pregiato”). – DSB XIV, 49 f.